About frequencies in materials

The term “frequency” in the context of atomic and molecular movement refers to how often the atoms or molecules oscillate, vibrate, or rotate in a specific period of time. Frequency is a fundamental concept in physics and chemistry, particularly in understanding the behaviors of atoms and molecules at different energy levels. It is measured in hertz (Hz), which is equivalent to one cycle per second.

Atomic and Molecular Vibrations

Atomic Vibrations in Solids: In solid materials, atoms are arranged in a lattice structure and can oscillate around their equilibrium positions. The frequency of these vibrations is influenced by the stiffness of the bonds between atoms and the mass of the atoms themselves. Higher frequencies are typically observed with stiffer bonds and lighter atoms.
Molecular Vibrations: Molecules can have more complex modes of vibration due to the various ways atoms within a molecule can move relative to each other. For example, molecules can experience stretching, bending, or twisting motions, each with its own characteristic frequency. These vibrational frequencies are crucial for molecular identification in spectroscopy.

Rotational Movements

Molecular Rotation: Molecules in gas phase can rotate freely, and these rotations occur at specific quantized frequencies depending on the moment of inertia and the rotational constants of the molecule. Rotational spectroscopy studies these frequencies to gain insights into molecular structure and dynamics.

Temperature Effects

Impact of Temperature: The frequency of atomic and molecular vibrations can also be influenced by temperature. Generally, increasing temperature can increase the amplitude of vibrations but might also affect the frequencies slightly, particularly in complex systems where anharmonicity plays a role.

The concept of frequency, when applied to atoms and molecules, describes the rate at which these particles move back and forth or rotate, under the influence of thermal energy, quantum mechanical forces, or electromagnetic radiation. This understanding allows us to probe the structure, properties, and interactions of materials and molecules at the microscopic level.

Using Frequency Interferences to our benefit

Constructive Interference:

Constructive interference occurs when two or more waves meet in such a way that their crests and troughs align perfectly, leading to an increase in wave amplitude. This type of interference results in a stronger or reinforced wave.

Destructive Interference:

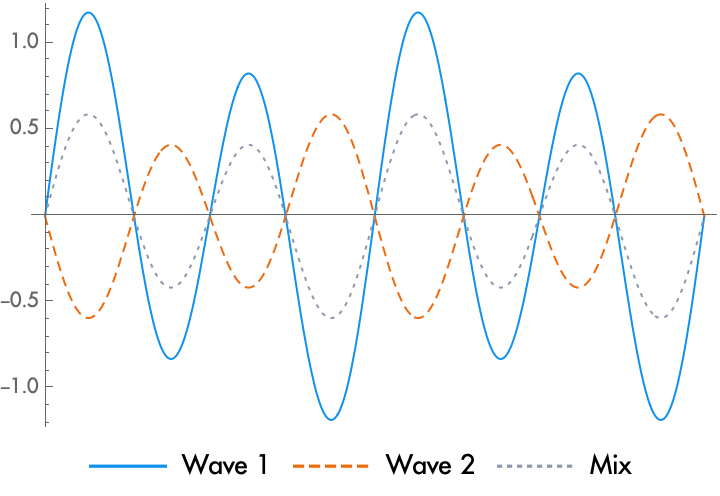
Destructive interference happens when two waves meet in such a way that the crest of one wave aligns with the trough of the other, effectively canceling each other out. This results in a reduced or zero amplitude.

These principles of wave interference we can use to our benefit in the field of physics.

The terms “natural frequency” and “eigenfrequency” often appear in the context of mechanical systems, structures, and vibrational analysis. Both terms are closely related and often used interchangeably in engineering and physics, but they can have slightly different connotations depending on the context.

Natural Frequency

The natural frequency of a system is the frequency at which the system tends to oscillate in the absence of any driving or damping force. This is a fundamental property of dynamic systems and is determined by the system’s physical characteristics such as mass, stiffness, and inherent damping. The natural frequencies are important in understanding how a system will respond to various external influences.

Eigenfrequency

Eigenfrequency is a term often used synonymously with natural frequency, especially in the context of solving differential equations that describe system dynamics. In mathematical terms, eigenfrequencies are obtained from the eigenvalues of the differential equations governing the system’s motion. These are the frequencies at which the system’s mode shapes (eigenvectors) occur, where mode shapes describe the patterns of motion the system undergoes when vibrating at each eigenfrequency.

Differences

While both terms describe similar concepts, the subtle differences are mainly in usage:

Natural Frequency: More commonly used in engineering, especially when discussing the physical response of a system.
Eigenfrequency: Often used in a more mathematical or theoretical context, particularly when discussing solutions to differential equations and the associated eigenvalues and eigenvectors.

In mechanical systems, these frequencies are key to ensuring that mechanical systems operate safely and efficiently, avoiding resonance conditions that could lead to excessive vibrations or system failure.

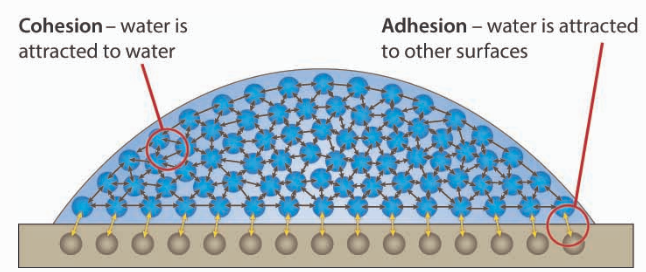
In the field of water treatment and biofilm prevention we use the resonance frequencies to either attach or detach particles using the effects of cohesion (water molecules between themselves) or adhesion (between water molecules and a surface) . These effects can be used to loosen-up molecules or change their properties in order to solve specific contamination problems.

Liquids can have resonant frequencies, although the nature of these frequencies and the ways they manifest can differ from those in solids and gases due to the fluid dynamics involved.

Understanding Resonant Frequencies in Liquids

Resonant frequencies in liquids are related to the natural vibrations that can be sustained within the fluid. These are typically associated with wave-like movements such as surface waves on the liquid or acoustic waves transmitted through the liquid. The resonant frequencies depend on several factors:

Physical Dimensions: Just like in solid objects, the shape and size of the container holding the liquid can significantly influence the resonant frequencies. The dimensions determine the possible wavelengths of standing waves that can form within the liquid.
Acoustic Properties: Liquids have specific acoustic properties, including density and bulk modulus (a measure of compressibility), which influence how sound waves propagate through the medium. The speed of sound in a liquid is given by $c = ρ B$ , where $B$ is the bulk modulus and $ρ$ is the density. The resonant frequencies for sound waves in a liquid container can be calculated based on these properties and the geometry of the container.
Boundary Conditions: The way the liquid interacts with its container’s walls (whether the walls are rigid or flexible) also affects its resonant frequencies. Additionally, the surface tension at the liquid-air interface can influence the dynamics of surface waves.

Examples of Resonant Frequencies in Liquids

Seismic Waves in Oceans: Ocean waves can exhibit resonance effects under certain conditions, such as in bays or harbors where the geometry can trap waves, causing them to amplify.
Acoustic Resonance: Liquids in containers can exhibit acoustic resonance. For example, when you tap a glass filled with water, the sound produced can change in pitch based on the amount of water in the glass. This change is due to the different resonant frequencies supported by different water levels.
Ultrasonic Applications: In ultrasonics, liquids are often used in cleaning and medical imaging applications where the resonant frequencies of the liquid help in transmitting high-energy acoustic waves effectively.